Der Methodenkoffer von Six Sigma ist vielfältig, hier einige Beispiele:
Meßsystemanalyse: Six Sigma ist datenbasiert - entsprechend muß sichergestellt werden, dass die Daten mit hinreichender Präzision ermittelt werden und die durch Meßprozessschwankungen (z.B. durch verschiedene Mitarbeiter) verursachten Variationen klein sind verglichen mit dem zu messenden Effekt.
Man sucht bei Six Sigma nach den "Hebeln", die sich möglichst stark auf die Variation der Zielgrößen auswirken. Die Methode: eine Kombination von Expertenwissen (dem Projektteam) und statistischen Werkzeugen - der Korrelationsanalyse.
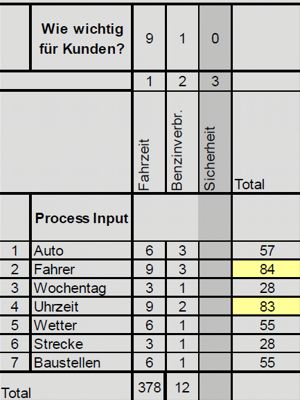
Die Dokumentation des Expertenwissens erfolgt am einfachsten über eine Ursache-Wirkungs-Matrix (Cause and Effect Matrix, C&E-Matrix). Die Eingangsparameter werden senkrecht aufgetragen - waagerecht die Zielgrößen (CTQs) des Kunden nebst deren Wichtung. Experten halten nun fest, welchen Einfluß die Eingangsparameter auf die Zielgrößen haben (von 0 = keiner bis 9 = sehr stark). Die gewichteten Faktoren (z.B. 9x6 + 3x1 = 57) geben einen Anhalt, welche Eingangsparameter eingehender untersucht werden sollten (gelb markiert).
Das (fiktive) Beispiel bezieht sich auf Fahrtzeiten zwischen Wohnung und Arbeitsplatz.
Sicherheitsrelevante Aspekte eignen sich nicht für eine derartige Priorisierung.
Korrelationsanalysen:
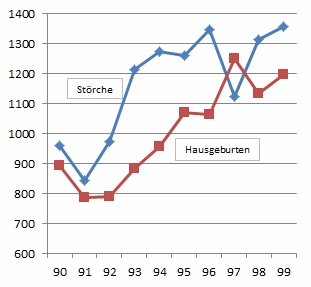
Schon das Auftragen verschiedener Parameter liefert dem Auge eine Korrelation ...
Dabei ist die Korrelation zwar eine notwendige, aber nicht eine hinreichende Bedingung für einen Kausalzusammenhang. Die Korrelation zwischen den Storchpopulationen und der Zahl der Geburten ist ein sprichwörtliches Beispiel. Eine lesenswerte Publikation zu diesem Thema finden Sie hier: http://web.stanford.edu/class/hrp259/2007/regression/storke.pdf
Die Darstellung zeigt aber auch, daß das Auge nicht immer das beste Werkzeug ist, um Korrelationen zu erkennen. Die richtige Vorgehensweise sind Korrelationsdiagramme bzw. entsprechende Tabellen, aus denen die Korrelationskoeffizienten und deren Vertrauensintervalle hervorgehen.
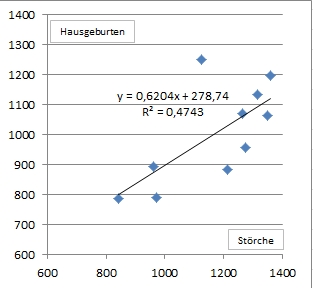
Die den Darstellungen zugrunde liegenden Daten stammen aus Berlin und Brandenburg - interessanterweise korreliert die Zahl der Geburten in den Kliniken nicht mit der Anzahl der Störche.
Die Frage, ob ein kausaler Zusammenhang besteht, ist in der Regel im Expertenkreis zu ermitteln (wenn er nicht aus technischen Gründen offensichtlich gegeben ist). Alternativ könnten auch die beiden betrachteten Größen auf eine gemeinsame Ursache zurückgeführt werden.
Solche Korrelationsdiagramme lassen sich auch für viele Parameter gemeinsam erstellen. Bei großen Datenmengen bietet sich die Darstellung als Heatmap an.
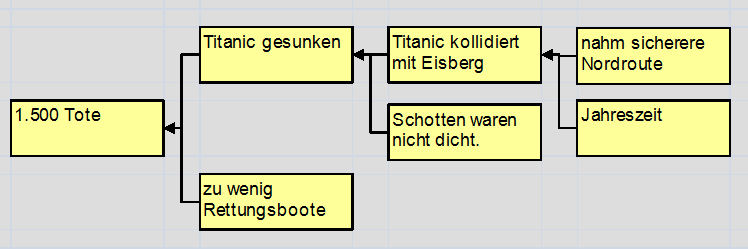
Root Cause Analyse (die Suche nach der zugrundeliegenden Ursache): ergänzt die Korrelationsdaten durch die Expertise der Experten für diesen Prozess. Dieses mehr qualitative Werkzeug bildet zusammen mit den Korrelationsdaten die Basis für die Verbesserung des Prozesses.
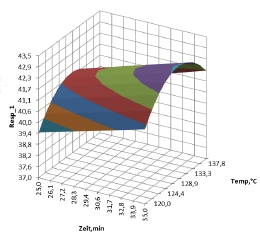
Modellentwicklung für den Prozeß: Zur Verifizierung der gefundenen Abhängigkeiten und zur Optimierung werden im Rahmen von Six Sigma "Designs of Experiments" (DoE) genutzt. Durch optimal ausgewählte Werte für die wichtigsten Eingangsparameter kann mit minimalem Aufwand ein Modell für die Zielgrößen ermittelt werden, daß sich z.B. als Response Surface Kurve darstellen läßt.
DoEs erlauben es, zunächst mit relativ kleinem Aufwand den Parameterraum ("reduzierte Faktor-Versuchspläne") abzustecken und durch zusätzliche Versuche das Modell für die Zielgrößen zu verbessern (z. B. mit der Erfassung von Nichtlinearitäten).

