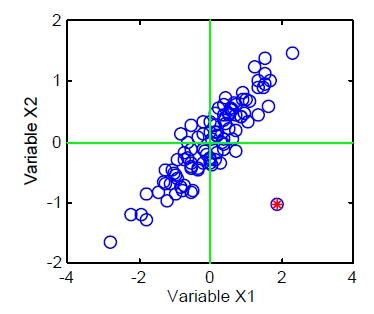
Multivariate Daten
In der Praxis sind die Eingangsgrößen Xi nicht immer voneinander unabhängig - sie korrelieren untereinander. Dies bedeutet auch, daß das System weniger Freiheitsgrade hat als der Zahl der Eingangsgrößen entspricht. Um dies angemessen in der Modellbildung zu berücksichtigen, verwendet man orthogonale Linearkombinationen der Eingangsgrößen ("principal components"), die ihrerseits als unabhängige Variable z. B. in Regressionsanalysen eingesetzt werden können. Die Zahl der verwendeten Principal Components richtet sich nach der geforderten Qualität des Modells und liegt in der Regel unter der Zahl der verwendeten Eingangsgrößen.
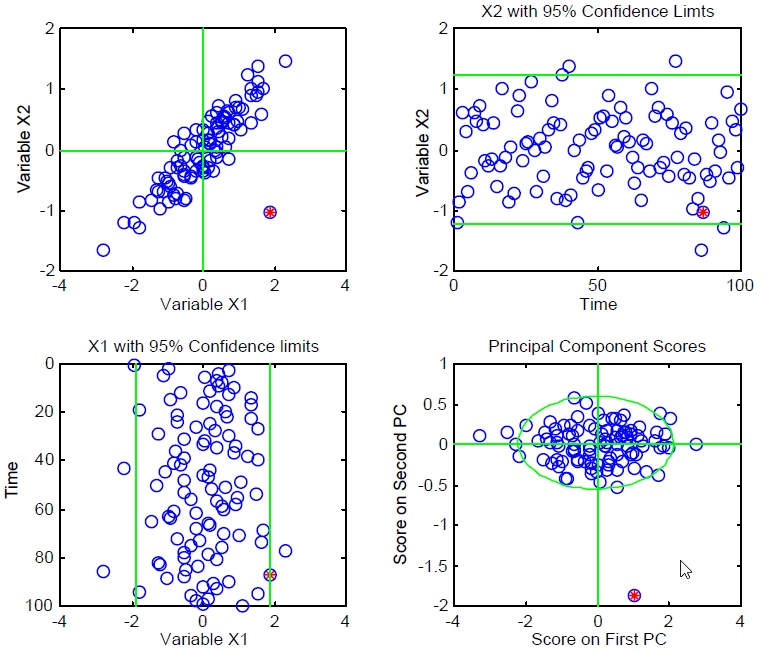
Multivariate Spezifikationsgrenzen
Gleiches gilt auch für die Ausgangsgrößen Yi, die korreliert sein können. Eine einfache Spezifikation der jeweiligen Ausgangsgrößen (links unten und rechts oben) läßt Ausreisser nicht erkennen - die bei Auftragung der Korrelation bzw. bei einer Auftragung der Principal Components deutlich hervortreten.
Die Spezifikationsgrenzen in derartigen Fällen werden durch eine Ellipse beschrieben. Eine Beschreibung über rechteckige (unabhängige) Spezifikationsgrenzen würden entweder dazu führen, daß nicht-spezifikationsgerechtes Material ausgeliefert wird (bei einem großen Rechteck) oder viel spezifikationsgerechtes Material nicht zur Auslieferung käme (bei einem kleinen Rechteck innerhalb der Ellipse).
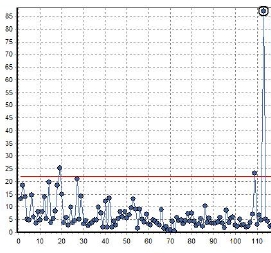
Multivariate Regelkarten
Wie ihre univariate Verwandte, Shewhart's SPCs, erlauben MVSPCs einen schnellen Überblick über Prozessveränderungen. Durch die Nutzung von Hotellings T² Statistik werden alle einbezogenen Parameter gleichzeitig und in ihrer Wechselwirkung berücksichtigt. Der entsprechende Control Chart (links) erlaubt es, multivariate Abweichungen, Veränderungen der Mittelwerte und Veränderung der Verteilungsfunktionen festzustellen - und festzustellen, auf welche Parameter diese zurückzuführen sind. Das Verfahren bietet sich somit als hochaggregiertes Warnsystem an, das aufgrund der Parameter-Zuordnung gleichzeitig ein wichtiges Analysetool ist. Zur Anwendung kommen MVSPCs sowohl zur Prozeß- als auch zur Qualitätsüberwachung.
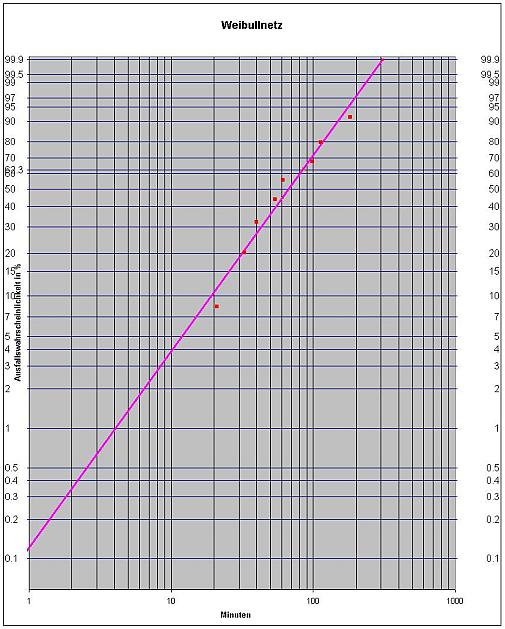
Zuverlässigkeitsanalysen
erfolgen unter Nutzung der Weibull-Statistik. Bei hohen Stückzahlen der gleichen Geräte läßt sich bei Vorliegen entsprechender Ausfalldaten eine Ausfallstatistik entwickeln, die sich z. B. für eine wirtschaftliche Abschätzung eignet. Bei Großanlagen der Prozessindustrie reicht die Datenbasis für derartige Abschätzungen meist nicht aus - das Verfahren eignet sich aber auch zur Abschätzung der Maximum Achievable Capacity (MAC) und der Maximum Sustainable Capacity (MSC).
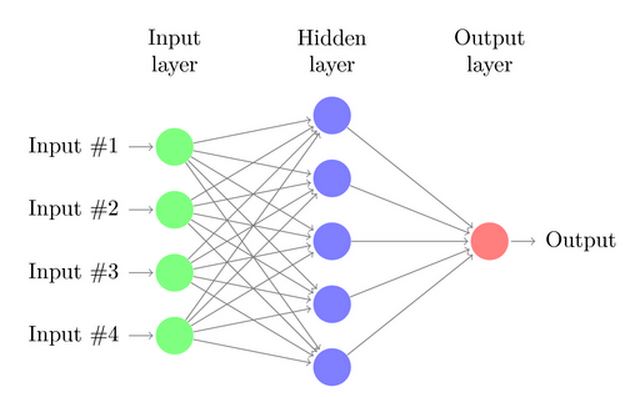
Black Box Modelle
Nicht immer gibt es bekannte physikalische Zusammenhänge zwischen den Parametern, nicht immer reichen einfache funktionale Zusammenhänge. Grundsätzlich ist es auch möglich, die Zielgrößen aus den Ausgangsparametern über Neuronale Netze zu ermitteln. Die Komplexität der zu verwenden Netze richtet sich dabei nach der Fragestellung. Die Netze sind zu trainieren und zu überwachen. Wie für alle Modelle gilt, dass sie nur in dem auch experimentell abgesicherten Bereich gültig sind. Mit solchen Modellen ist es auch möglich, nicht-lineare Regler zu konzipieren und umzusetzen.
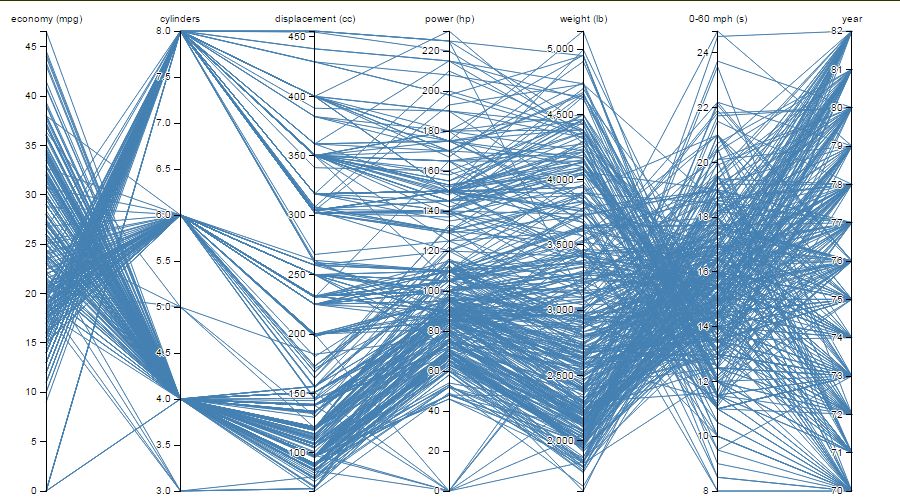
Parallelkoordinaten
Eine auf den ersten Blick ungewöhnliche Art, multivariate Zusammenhänge darzustellen, nutzt Parallelkoordinaten: Die einzelnen Parameter werden auf ihrer jeweils eigenen Achse abgebildet. Die Verbindung der einzelnen Parameterpunkte stellt jeweils einen Datensatz dar. Die Zahl der abzubildenden Parameter wird damit beinahe beliebig hoch. Durch geeignete Filter lassen sich multivariate Zusammenhänge ermitteln und zur Prozeßoptimierung nutzen.
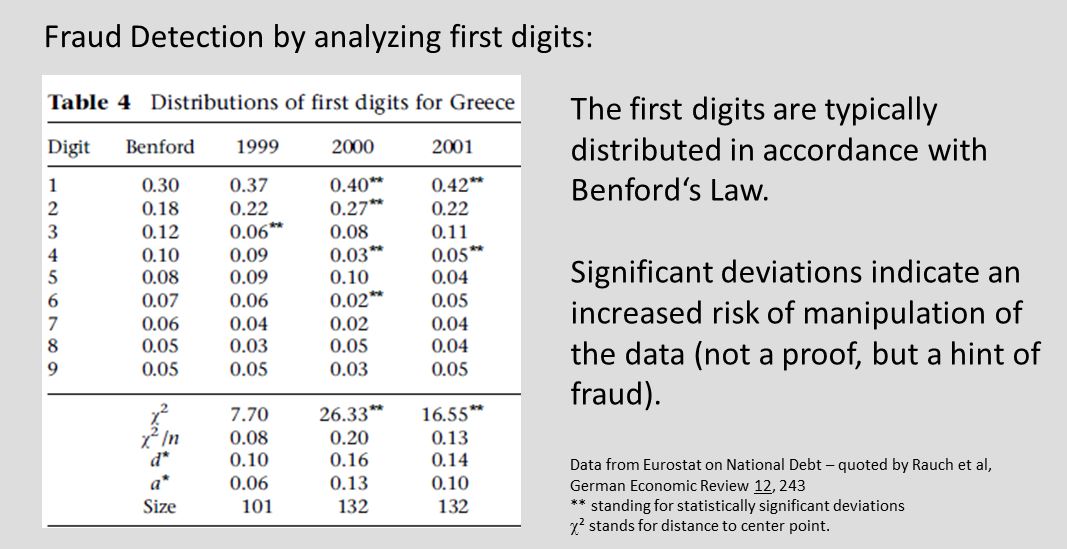
Benford's Law
Um einen Hinweis zu erhalten, ob Zahlen manipuliert wurden, lässt sich auf Benford's Law zurückgreifen. Die Verteilung z. B. der ersten Ziffern folgt bei hinreichend großen und hinreichend breit verteilten Datensätzen (möglichst über mehrere Zehnerpotenzen) keiner Gleichverteilung, sondern vielmehr einer logarithmischen Verteilung: Die Ziffer 1 sollte in ca. 30 % der Fälle auftreten, die Ziffer 2 in ca. 18 %, etc.
Die zur Euro-Einführung vorgelegten Zahlen der griechischen Statistikbehörden für das Jahr 2000 sind auffällig und hätten eine weitergehende Prüfung nahegelegt ...
Weitere Informationen zu Benfords Law finden Sie hier.

